BELİRSİZ İNTEGRAL
TANIM:
tanımlı ve türevlenebilir iki fonksiyon olsun.
Her x Є (a, b) için, F’(x) = f(x) ise F(x) fonksiyonuna f(x) fonksiyonunun ilkeli veya belirsiz integrali denir. Bunu, C Є R olmak üzere,
Biçiminde gösterilir. ſ f(x) dx ifadesini, “integral f(x) dx” diye okuruz.
Kısaca, ſ f(x) dx demek, türevi f(x) olan F(x) fonksiyonunu bulmak demektir.
ſ f(x) dx = F(x)+C ifadesindeki;
- f(x) fonksiyonuna integrand,
- F(x) fonksiyonunun bulunması işlemine integrasyon işlemi,
- C reel sayısına da integrasyon sabiti denir. Bir fonksiyonda, sabit terimin türevi sıfır olduğundan, integral alınırken bu sabit terimi bilemeyiz.
- ſ f(x) dx ifadesindeki dx ise, integrasyonyn değişkeninin x olduğunu belirtir.
TEOREM: Bir fonksiyonun diferansiyelinin integrali, bu fonksiyona sabit eklenerek bulunur.
ſ d( f(x) ) = f(x)+C dir.
TEOREM: Bir fonksiyonun bir sabitle çarpımının integrali, o fonksiyonun integralinin sabitle çarpımına eşittir.
Yani, integral içindeki sabit çarpan, integral dışına alınabilir.
Her a Є R için, ſ a . f(x) dx = a . ſ f(x) dx dir.
TEOREM: İki fonksiyonun veya farkının integrali, bu fonksiyonların integrallerinin toplamına veya farkına eşittir.
ſ[f(x) + g(x)] dx = ſ f(x) dx + ſ g(x) dx ,
ſ[f(x) - g(x)] dx = ſ f(x) dx - ſg(x) dx tir.
TEMEL İNTEGRAL ALMA FORMÜLLERİ
Yukarıdaki eşitliklerin doğruluğunu gösterebilmek için, sağ taraftaki fonksiyonların türevlerini alarak, integrali alınan fonksiyonu elde ederiz.
İNTEGRAL ALMA YÖNTEMLERİ
İntegrali alınacak fonksiyonun, hangi fonksiyonun türevi olduğunu görmek, her zaman pek mümkün olmaz. Bunun için, bazı integral alma yöntemleri oluşturulmuştur.
1. DEĞİŞKEN DEĞİŞTİRME YÖNTEMİ
f, g, fog ve g’ fonksiyonları, bir [a, b] aralığında sürekli fonksiyonlar olsun
ſ f(g(x)).g’(x) dx
biçimindeki integralleri hesaplamak için, u = g(x) dönüşümü yapılır ve her iki tarafın diferansiyeli alınırsa, du = g’(x) dx elde edilir. Bu durumda integral,
ſf(g)).g’(x) = ſ f(u) du
biçimine dönüşür. ſ f(u) du ifadesinin, u değişkenine göre integrali alındıktan sonra, u yerine g(x) yazılarak, sonuç x değişkenine göre bulunmuş olur.
* ſ [f(x)]ⁿ . f’8x) dx ifadesinde olduğu gibi, kuvveti alınan fonksiyonun türevini aldığımızda, yanındaki çarpanı elde edebiliyorsak, bu ifadenin integralini kısaca;
ſ[f(x)]ⁿ . f’(x) dx = {[f(x)]ⁿ´¹ / n+1} + C (n = -1)
biçiminde alabiliriz.
LOGARİTMİK VE ÜSTEL İNTEGRAL ALMA KURALLARI:
1. ſ {f´(x) / f (x) = ln |f (x)| + C
2. ſ eª . f´(x) dx = eª + C ( a = f(x))
3. ſ eª . f´(x) dx = {eª / ln e} + C (a = f(x))
Bu eşitliklerin, sağ tarafındaki ifadelerin türevlari alındığında, integrali alınacak ifade elde edilir.
BAZI TRİGONOMETRİK İFADELERİN İNTEGRALLERİ
1. ſ sin(f(x)) . f´(x) dx = -cos f(x) + C
2. ſ cos (f(x)) . f’(x) dx = sin f(x) + C
3. ſ{f’(x) / cos²f(x)} dx = tan f(x) + C
4. ſ{f’(x) / sin²f(x)} dx = -cot f(x) + C
5. ſsin(ax + b) dx = (-1 / a) cos(ax + b) + C (a = 0)
6. ſcos(ax + b) dx = (1 / a) sin(ax + b) + C (a = 0)
7. ſ{dx / cos²(ax + b) dx = (1 / a) tan (ax + b) + C (a = 0)
8. ſ{dx / sin²(ax + b) dx = (-1 / a) cot (ax + b) + C (a = 0)
9. ſcot (ax + b) dx = ſ{cos (ax + b) / sin (ax + b) dx = (1 / a) ln |sin(ax + b)| + C
Yukarıdaki eşitliklerde, sağ taraftaki fonksiyonların türevlvri alındığında, integrali alınan fonksiyon elde edilir.
2 KISMİ (PARÇALI) İNTEGRASYON YÖNTEMİ
İki fonksiyonun çarpımının integralinin hesaplanmasında genelde, kısmi integrasyon yöntemi kullanılır.bilgiyelpazesi.com
u ve v fonksiyonları, bir (a,b) aralığında türevlene bilen fonksiyonlar ise, u, v fonksiyonu da (a, b) aralığında türevlidir.
{(d / dx)(u . v)} = {(du v / dx) + (dv u / dx) olduğundan,
d(u . v) = v du + u dv ve
u dv = d(u . v) – v du olur.
Bu eşitliğin her iki yanının integralini alırsak;
ſ u dv = u . v - ſ v du olur.
Bu yöntemle integral almaya, kısmi integrasyon yöntemi denir.
3 BASİT KESİRLERE AYIRMA YÖNTEMİYLE İNTEGRAL ALMA
P(x) ve Q(x) birer polinom olmak üzere, {P(x) / Q(x)}, (Q(x) = 0) biçimindeki fonksiyonlar, rasyonel fonksiyonlardır. Basit kesirlerine ayrılabilen rasyonel fonksiyonların integralleri şu şekilde bulunur:
a, b, c, A, B Є R ve n Є N olsun. (A / (ax + b)ⁿ) ve Δ< 0 olmak üzere,
{Ax + B / (ax² + bx + c)ⁿ biçimindeki ifadelere basit kesir denir. {P(x) / Q(x)}rasyonel ifadesi, basit kesirlerin tplamı biçiminde yazılabiliyorsa, yapılan işleme; basit kesirlere ayırma denir.
Rasyonel ifadelerin integralinin hesaplanmasında 2 yöntem vardır.
A. P(x) in Derecesi, Q(x) in Derecesinden Küçük ise
Bu durumda, aşağıdaki yollar izlenir:
a) {P(x) / Q(x)) rasyonel ifadesinin paydası olan Q(x),
Q(x) = (a x + b )(a x + b)…(a x + b) biçiminde r tane çarpandan oluşuyorsa, bu ifade:
{P(x) / Q(x)} = {A / a x + b} + {A / a x + b}+….+{A / a x +b} şeklinde basit kesirlerin toplamı olarak yazılır. Polinomların eşitliğinden yararlanılarak; A , A , ….., A değerleri bulunur ve sonrada integral alınır.
B. P(x) in Derecesi, Q(x) in Derecesinden büyük veya eşit ise
Bu durumda, P(x) polinomu Q(x) polinomuna bölünür. P(x) in Q(x) e bölünmesinden bulunan bölüm B(x) ve kalan K(x) ise,
{P(x) / Q(x)} = B(x) + {K(x) / Q(x)} biçiminde yazılır ve bu ifadenin integrali alınınr.
TRİGONOMETRİK ÖZDEŞLİKLER YARDIMIYLA İNTEGRAL ALMA
Bazı trigonometrik ifadelerin integralleri alınırken, ayşağıda verilen trigonometrik özdeşliklerden yararlanılır.
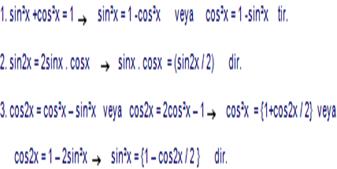
n Tek Doğal Sayı ise ſ sinⁿx dx veya ſ cosⁿx dx Biçiminde Verilen İntegralleri Hesaplama
ſ sinⁿ dx = ſ sinⁿ־¹x .sinx dx veya ſ cosⁿ dx = ſ cosⁿ־¹x .cosx dx biçiminde yazılır. Daha sonra,
sin²x = 1 - cos²x veya cos²x = sin²x özdeşlikleri yazılarak integral alınır.
n Çift Doğal Sayı ise ſsinⁿ dx veya ſ cosⁿx dx Biçiminde Verilen İntegrallerin Hesaplanması
ſsinⁿx dx = ſ(sin²x)ⁿ´² dx veya ſcosⁿx dx = ſ(cos²x)ⁿ´² dx yazılır.
Daha sonra, sin²x = (1 – cos2x / 2) veya cos²x = (1 + cos2x / 2) özdeşlikleri yazılarak integrali alınır.
İNTEGRAL FORMULLERİ
fonksiyonu verilmiş olsun.
ile gösterilir. Buna göre,
verilsin. 
olmak üzere,
fonksiyonu 
şeklinde belirtilebileceği gibi, g ve h iki fonksiyon olmak üzere
olmak üzere,
ifadesine
ifadesine de y = f(x) in n.
